Simple Linear Regression

Linear regression is a supervised machine learning algorithm used for predictive analysis. The Linear Regression algorithm predicts the value of a variable y based on the value of one or more quantitative variable x = (x1, x2, … xn), where y is a dependent (or outcome) variable and x is an independent (or predictor or explanatory) variables.

Simple Linear Regression is a commonly considered analysis method when examining the relationship between a quantitative outcome y and a single quantitative independent variable x.

The structural model underlying a simple linear regression analysis is that the independent variable x and outcome variable y are linearly related such that the population mean of the outcome for any x value is ax + b. It is represented as 


      ---Output---
      #     E(y|x) = ax + b
      # where
      #     E(), “expected value of”
      #     y|x, “y given x”,indicates the possible values of y when x is restricted to some single value
      #     a, slope parameter
      #     b, intercept parameter

The slope represents the change in the dependent variable for a unit change in the independent variable. The intercept is the value of the dependent variable when the independent variable is zero.

The goal of Linear Regression is to find the best-fitting line that minimizes the difference between predicted and actual values.

Simple Linear Regression

This module covers the following steps:

  ➤ 1. Import the required libraries

  ➤ 2. Read the data for Linear Regression analysis

  ➤ 3. Understanding the data

  ➤ 4. Split the data into train and test sets

Simple Linear Regression

↪ 1. Import the required libraries

Pandas is a Python library that is used to work with data sets. When working with tabular data, such as data stored in spreadsheets or databases, pandas give the APIs to explore, clean, and process the data. In Pandas, a data table is called a DataFrame. Reference: https://pandas.pydata.org/

Matplotlib is a Python library for creating static, animated, and interactive visualizations in Python. The pyplot submodule contains most of the Matplotlib utilities. Reference: https://matplotlib.org/

Seaborn is a Python data visualization library based on matplotlib. It provides a high-level interface for drawing attractive and informative statistical graphics. It provides data visualizations that are more aesthetic, statistically sophisticated, and offer more appealing default color palettes. Reference: https://seaborn.pydata.org/

Scikit-learn (sklearn) is a machine-learning Python library that supports supervised and unsupervised learning. The sklearn provides statistical tools for data preprocessing, model design, and analysis. Reference: https://scikit-learn.org/stable/

Statsmodels is a Python module that provides classes and functions for the estimation of many different statistical models, as well as for conducting statistical tests, and statistical data exploration. Reference: https://www.statsmodels.org/stable/api.html 

      import pandas as pd                                 # Matplotlib is the fundamental plotting library
      import matplotlib.pyplot as plt                     # Seaborn builds upon Matplotlib, offering a
      import seaborn as sns                               # higher-level interface for statistical visualization.

Set default style and color scheme for Seaborn plots. 

      sns.set(style="ticks", color_codes=True)
  • style=”ticks”: This sets the plot style to “ticks,” which typically includes gridlines and tick
    • marks, giving the plot a more structured look.
  • color_codes=True: This enables the use of Seaborn's built-in color palettes, which are generally
    • considered more visually appealing than Matplotlib's defaults.

    Simple Linear Regression

    ↪ 2. Read the data for Linear Regression analysis

    The read_csv() method of the Pandas library can be used to read a CSV file. 

          data = pd.read_csv('https://raw.githubusercontent.com/csxplore/data/main/andromeda-cleaned.csv', 
                       header=0)

    The objective of this module is to demonstrate simple linear regression to predict “Close Price” of the stock from the previous day's close price. That is to say, “Close Price” is the dependent variable, and “Prev Close” is the independent variable.

    So, select just the relevant columns below for further analysis. 

          data = data[['Prev Close','Close Price']]
      print(data.head(5))

          ---Output---
      # -   Prev Close  Close Price
      # 0     1401.55      1388.95
      # 1     1388.95      1394.85
      # 2     1394.85      1385.10
      # 3     1385.10      1380.30
      # 4     1380.30      1378.45

    Simple Linear Regression

    ↪ 3. Understanding the data

    The data should exhibit the following characteristics for successful regression analysis and model building.

  • The data must not include one or a few extreme values (Outliers).
  • The relationship between x and y should be linear (Linearity).
  • All the observations are independent of each other (Independence).

    • If these assumptions are not met, linear regression analysis may produce misleading results, potentially creating a false sense of relationship in the data even when none exists.

    Simple Linear Regression

    ↪ 3. Understanding the data

    i.a. Finding outliers using IQR

    The describe() method of Pandas DataFrame returns a description of the data in the DataFrame. 
          print(data.describe(include = 'all'))   #parameter include=all will display NaN values as well

          ---Output---
      # -        Prev Close  Close Price
      # count   250.000000   250.000000
      # mean   1536.385800  1537.268600
      # std     112.143024   111.947898
      # min    1281.300000  1281.300000
      # 25%    1439.100000  1440.512500
      # 50%    1579.825000  1582.325000
      # 75%    1631.087500  1631.087500
      # max    1727.800000  1727.800000

    The result’s index includes count, mean, std, min, percentiles, and max values. The data set has 250 observations.

    By default, the lower percentile or first quartile is 25 and the upper percentile or third quartile is 75. Q1 and Q3 represent the first and third quartiles, respectively.

    The 50 percentile is the same as the median. 

          # IQR is the Interquartile Range (IQR = Q3 - Q1), which is
      #     IQR for Prev Close  = 1631 - 1439 = 192
      #     IQR for Close Price = 1631 - 1440 = 191

    Values above Q3 + (1.5 x IQR) or below Q1 – (1.5 x IQR) are considered as outliers. 

          #     For Prev Close: min = 1281, max = 1727
      #         Q3 + (1.5 x IQR) = 1631 + (1.5 x 192) 
      #                          = 1919, which is greater than max ie. no outliers at the upper bound
      #
      #         Q1 - (1.5 x IQR) = 1281 - (1.5 x 192)
      #                          = 993, which is less than min ie. no outliers at the lower bound
      #
      #     For Close Price: min = 1281, max = 1727 
      #         Q3 + (1.5 x IQR) = 1631 + (1.5 x 191) 
      #                          = 1917.5, which is greater than max ie. no outliers at the upper bound
      #
      #         Q1 - (1.5 x IQR) = 1281 - (1.5 x 191)
      #                          = 994.5, which is less than min ie. no outliers at the lower bound

    Values above Q3 + (3 x IQR) or below Q1 – (3 x IQR) are considered extreme points (or extreme outliers). In the data set, no outliers or extreme outliers are found.

    Simple Linear Regression

    ↪ 3. Understanding the data

    i.b. Finding outliers using Boxplots

    Boxplots are a popular and easy method for identifying outliers. The boxplot is an effective tool to visualize the data spread with respect to central values, and it shows the min, max, median, first quartile, and third quartile. 
          vars = ['Prev Close', 'Close Price']
 
      for v in vars:
          sns.boxplot(x=v, data=data)
          plt.title(v)
          plt.show()
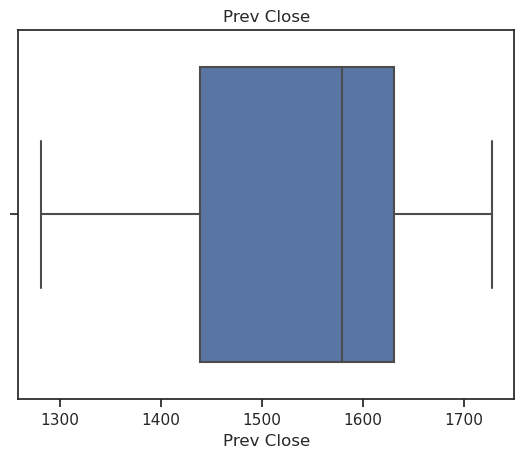
    Previous Close
    Close Price

    Simple Linear Regression

    ↪ 3. Understanding the data

    ii. Linear Relationship

    A correlation analysis in linear regression models provides information on the strength and direction of the linear relationship between the dependent and independent variables.

    Correlation heatmaps are a type of plot that visualizes the strength of relationships between numerical variables. 

          corr = data.corr()
      sns.heatmap(corr, vmin=None, vmax=None, cmap=None, 
                  center=None, annot_kws= None, linewidths=0.5, 
                  linecolor = 'black', cbar=True, annot=True)
      plt.show()
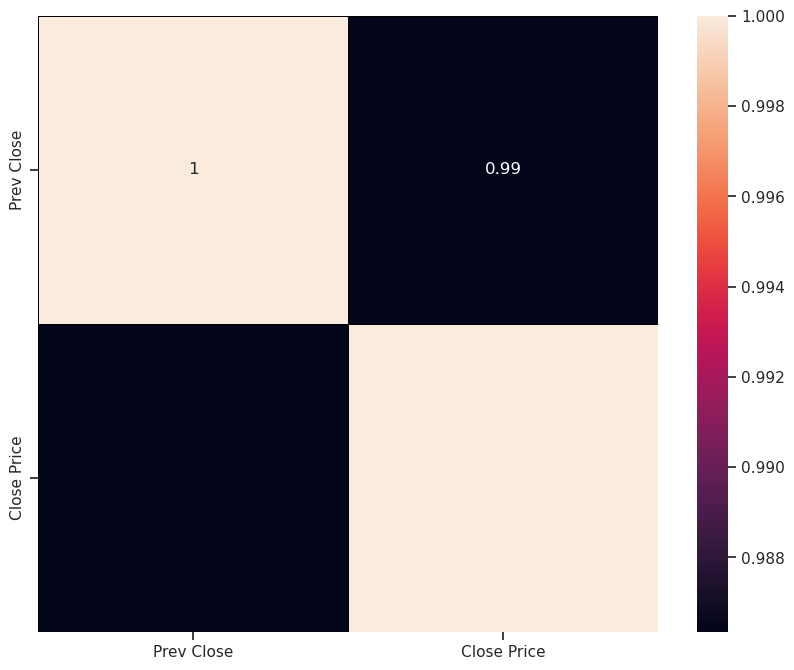
    Correlation heatmaps

    A correlation coefficient provides a measure of the strength of linear association – a measure of how closely the individual data points lie on the regression line.

    The value of the correlation coefficient can take any value from -1 to 1.

  • If the value is 1, it is said to be a positive correlation between two variables. This means that when one variable increases, the other variable also increases.
  • If the value is -1, it is said to be a negative correlation between the two variables. This means that when one variable increases, the other variable decreases.
  • If the value is 0, there is no correlation between the two variables. This means that the variables changes in a random manner with respect to each other.

    • The correlation coefficient of 0.99 between “Prev Close” and “Close Price” indicates a strong linear relationship between them.

    Simple Linear Regression

    ↪ 3. Understanding the data

    iii. Independence

    The data set is a record of the closing price of a stock where the price information of the same stock was collected over time. This type of dataset is called a Longitudinal dataset, and this type of dataset must pass the independence test.

    ⚠ HOTS

    There are two types of data studies: Cross-sectional and Longitudinal.

  • Cross-sectional studies are studies based on data collected on entities only once at a specific time.
  • Longitudinal studies are those studies based on the data where the data is collected on entities over time.

    • A residual time series plot (residuals vs. fitted line) or plot of residual autocorrelations will help to confirm the independence of observations. This test will be covered in the later section.

    Scatter plots are a powerful tool for visually assessing data independence, and they can help identify patterns, clusters, outliers, and potential relationships between variables.

    The regplot() method in the seaborn package is used to draw a scatter plot and a linear regression model fit. This helps to emphasize patterns in a dataset. The plot below shows the resulting regression line of x and y and a 95% confidence interval for that regression. 

          x=data[['Prev Close']]
      y=data[['Close Price']]
      sns.regplot(x=x, y=y, ci=90,
                  scatter_kws = {"color": "black", "alpha": 0.5},
                  line_kws = {"color": "red"})
      plt.show()
    Data Independence

    Remember that, it's essential to consider other statistical methods and context to understand fully the nature of the relationship between variables.

    While the seaborn package makes exploring a dataset through visualization quick and easy, the statsmodels should be used to obtain quantitative measures related to the fit of regression models. The regplot() method in the seaborn is primarily intended to add a visual guide that helps to emphasize patterns in a dataset during exploratory data analyses.

    Simple Linear Regression

    ↪ 4. Split the data into train and test sets

    Supervised machine learning is about creating models that precisely map the given inputs (explanatory, predictors, independent variables) to the given outputs (responses, dependent variables).

    The train test split is a model validation procedure that allows the machine to simulate how a model would perform on new or unseen data. A goal of supervised learning is to build a model that performs well on new data.

    The train_test_split() method is used to split the data into train and test sets. 

          from sklearn.model_selection import train_test_split 
      x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.2,random_state=0)

    The dataframe is divided into x_train, x_test, y_train, and y_test. The x_train and y_train sets are used for training and fitting the model. The x_test and y_test sets are used for testing the model. The train sets should be larger than the test sets. 

          print("x_train.shape: ", x_train.shape )
      print("x_test.shape: ", x_test.shape )
      print("y_train.shape: ", y_train.shape )
      print("y_test.shape", y_test.shape )

          ---Output---
      # x_train.shape:  (200, 1)
      # x_test.shape:  (50, 1)
      # y_train.shape:  (200, 1)
      # y_test.shape (50, 1)