Fit the model using the statsmodels OLS library
This module covers the following steps:
➤ 1. Preparing Data for Regression Analysis
➤ 2. Importing statsmodels Library
➤ 3. OLS Regression results
➤ 4. Model Summary
➤ 5. Coefficients Table
➤ 6. Potential Issues
➤ 7. Residual Analysis
➤ 8. Predict and test the model
Fit the model using the statsmodels OLS library
↪ 1. Preparing Data for Regression Analysis
Import the pre-processed data for analysis. Subsequently, the data will be partitioned into training and test sets to facilitate the analysis.
# Import required libraries
import pandas as pd # Matplotlib is the fundamental plotting library
import matplotlib.pyplot as plt # Seaborn builds upon Matplotlib, offering a
import seaborn as sns # higher-level interface for statistical visualization.
import numpy as np
# Import data
data = pd.read_csv('https://raw.githubusercontent.com/csxplore/data/main/andromeda-cleaned.csv',
header=0)
data = data[['Prev Close','Close Price']]
x=data[['Prev Close']]
y=data[['Close Price']]
# Set default style and color scheme for Seaborn plots
sns.set(style="ticks", color_codes=True)
# Split the data into training and test sets
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.2,random_state=0)
Fit the model using the statsmodels OLS library
↪ 2. Importing statsmodels Library for OLS Regression
The statsmodels library, by default, fits a line through the origin. To include an intercept, manually add a constant to the x_train dataset using the add_constant attribute of statsmodels.
After adding the constant, fit a regression line using the OLS (Ordinary Least Squares) attribute of statsmodels.
import statsmodels.api as sm x_train_sm = sm.add_constant(x_train) # Add a constant to get an intercept lr = sm.OLS(y_train, x_train_sm).fit() # Fit the regression line using 'OLS'
A fitted model's params property provides the slope and intercept values.
print(lr.params)
---Output--- # const 16.587365 # Prev Close 0.990746 # dtype: float64
In the output, 'const' represents the intercept, and 'Prev Close' represents the slope for 'Close Price'.
Fit the model using the statsmodels OLS library
↪ 3. OLS Regression results
The summary() method summarizes the regression results.
print(lr.summary())
---Output--- # OLS Regression Results # ============================================================================== # Dep. Variable: Close Price R-squared: 0.977 # Model: OLS Adj. R-squared: 0.977 # Method: Least Squares F-statistic: 8279. # Date: Wed, 25 Oct 2023 Prob (F-statistic): 1.71e-163 # Time: 20:19:48 Log-Likelihood: -854.93 # No. Observations: 200 AIC: 1714. # Df Residuals: 198 BIC: 1720. # Df Model: 1 # Covariance Type: nonrobust # ============================================================================== # coef std err t P>|t| [0.025 0.975] # ------------------------------------------------------------------------------ # const 16.5874 16.749 0.990 0.323 -16.442 49.617 # Prev Close 0.9907 0.011 90.987 0.000 0.969 1.012 # ============================================================================== # Omnibus: 26.996 Durbin-Watson: 1.953 # Prob(Omnibus): 0.000 Jarque-Bera (JB): 66.459 # Skew: 0.577 Prob(JB): 3.70e-15 # Kurtosis: 5.578 Cond. No. 2.09e+04 # ==============================================================================
Fit the model using the statsmodels OLS library
↪ 4. Model Summary
Dep. variable The 'Close Price' is a dependent variable dependent on the variable 'Prev Close'.
Model/Method The Ordinary Least Squares (OLS) method provides the best approximation of the true population regression line by minimizing the sum of squared errors.
Degrees of freedom Degrees of freedom determine the shape of the t-distribution, which is used in t-tests to calculate p-values.
Sets with lower degrees of freedom have a higher probability of extreme values. Conversely, sets with higher degrees of freedom, such as a sample size of 30 or more, approach a normal distribution. Smaller sample sizes correspond to fewer degrees of freedom and result in wider (fatter) t-distribution tails.
From the summary table above,
Number of observations (it is the size of data) = 200
Degrees of freedom (Df) (it is Df of residuals) = 198
Df of model = 1
⚠ HOTS
Degree of freedom(df) of residuals:
Degrees of freedom represent the number of independent observations used to calculate the sum of squares.
# K = (number of variables + 1) = (1 + 1) = 2 # Df Residuals = No. of observations - K # = 200 – (2) = 198 # # Df of model = (K - 1) # Df of model = (2 – 1) = 1
Fit the model using the statsmodels OLS library
↪ 4. Model Summary
Covariance Type The “Covariance Type” in OLS regression refers to the method used to estimate the covariance matrix of the regression coefficients. This matrix is crucial for calculating standard errors, t-statistics, and confidence intervals.
The nonrobust method assumes that the errors in your model are homoscedastic (have constant variance) and uncorrelated.
Other Covariance Types are:
Fit the model using the statsmodels OLS library
↪ 4. Model Summary
R-squared and Adj. R-squared The coefficient of determination, R-squared (R²), measures how well a statistical model predicts an outcome.
Because the model includes only one independent variable, the adjusted R-squared is identical to the regular R-squared. The adjusted R-squared is particularly useful when comparing models with different numbers of independent variables or multiple regression models with several predictors.
F-statistic and Prob (F-statistic) While R-squared tells about the proportion of variance explained by the model, F-statistic tests the statistical significance of the overall model, indicating if the independent variables as a whole have a meaningful effect on the dependent variable.
The F-statistic tests the hypothesis of a linear regression model's existence. This is done by setting up a null hypothesis. The following example illustrates the hypothesis definition for a linear regression model.
# y = β0 + β1.x1, where # y is the dependent variable, # x1 is an independent variable, and # β1 is a coefficient to be estimated for x1 # # Then, the null and alternate hypotheses can be written as: # H0: β1 = 0, Regression model does not exist # Ha: β1 ≠ 0, Regression model exists
A higher F-value indicates stronger evidence against the null hypothesis. This means that the independent variables collectively explain a significant portion of the variation in the dependent variable. A value of 8279 is high, suggesting strong evidence against the null hypothesis.
A low p-value (typically less than 0.05) suggests that there is sufficient evidence to reject the null hypothesis and to conclude that the model as a whole is statistically significant. The p-value of 1.71e-163 is much less than 0.05, providing strong evidence to reject the null hypothesis.
Fit the model using the statsmodels OLS library
↪ 4. Model Summary
AIC and BIC Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) are two model selection criteria used in statistical modeling. AIC and BIC are calculated for different models by varying the sets of independent variables included.
A model with more independent variables is generally more complex. While a more complex model can often achieve a higher R-squared, it may overfit the data.
R-squared measures the goodness of fit, indicating the proportion of variance explained by the model. Meanwhile, AIC and BIC consider model complexity. By comparing R-squared, AIC, and BIC across different models, one can determine the optimal balance between goodness of fit and model complexity.
Log-Likelihood Log-likelihood measures how well a model fits the data, taking into account the model's complexity. A higher likelihood indicates that the model is more likely to have produced the observed data. Log-likelihood is simply the natural logarithm of the likelihood.
Log-likelihood values from different models can be directly compared when the models have the same number of observations. However, log-likelihood values are often used in conjunction with AIC and BIC.
A higher log-likelihood value generally indicates a better fit.
Fit the model using the statsmodels OLS library
↪ 5. Coefficients Table
coef From the summary table, Intercept: The values of const coef = 16.5874 Slope: The values of 'Prev Close' coef = 0.9907 So, the linear equation of the fitted line is y = 0.9907x + 16.5874
std err The standard error of the regression slope, often called the standard error of regression (SER), provides a measure of the uncertainty in the estimated slope of a linear regression model.
The SER, which is 0.011, measures the variability around the estimated regression slope. It is used to calculate the t-statistic for the predictor variable “Prev Close”.
Fit the model using the statsmodels OLS library
↪ 5. Coefficients Table
t-distribution and p-value The t-distribution is a probability distribution resembling the normal distribution with its bell shape, but it has heavier tails. This means t-distributions have a greater chance for extreme values than normal distributions, resulting in fatter tails and higher kurtosis.
The t-statistic is used in a t-test to determine whether to support or reject the null hypothesis.
If the null hypothesis is
H0 : Prev Close = 0 ( variable Prev Close does not influence Close Price)
Ha : Prev Close ≠ 0 ( Prev Close has a significant impact on Close Price)
From the summary table, the t-score of “Prev Close” or slope variable is 90.987.
⚠ HOTS
Recall that the linear equation defined earlier, which is E(y|x) = ax + b i.e. y = 0.9907x + 16.5874, and from the summary table Std error (SER) of the slope parameter = 0.011, and A standard normal distribution has a mean (M) of 0, then A t-score of the slope term is calculated as t = (a – M)/SER(a) = (0.9907 – 0) / 0.011 = 90.987
In the summary table above, the P>|t| value for the slope parameter is 0.000. This indicates that the probability of obtaining a t-value of 90.987 or greater, assuming the null hypothesis is true, is extremely low. Therefore, we reject the null hypothesis and conclude that the alternative hypothesis – that “Prev Close” has a significant impact on “Close Price” – is supported by the data.
⚠ HOTS
A p-value is the probability of getting a result equal to or greater than what was observed, assuming that the Null hypothesis is true. In simpler terms, the p-value indicates the likelihood that the observed results occurred due to random chance.
A p-value measures the strength of the evidence against H0:
Fit the model using the statsmodels OLS library
↪ 5. Coefficients Table
Confidence Interval The column labeled “[0.025 0.975]” represents the 95% confidence interval for each regression coefficient.
The confidence interval in the above table is 0.969 and 1.012, which means 95% confidence that the true population coefficient for the impact of 'Prev Close' on 'Close Price' lies between 0.969 and 1.012.
Since the confidence interval does not include zero, the coefficient is statistically significant at the 95% level i.e. 'Prev Close' has a statistically significant impact on 'Close Price'.
Fit the model using the statsmodels OLS library
↪ 6. Potential Issues
Omnibus and Prob(Omnibus) The Omnibus test assesses the normality of the residuals: the difference between the actual values and the predicted values in a regression model are normally distributed. The test utilizes a combination of skewness and kurtosis: skewness measures the asymmetry of the distribution, while kurtosis measures its “tailedness.”
The null and alternate hypotheses can be written as:
H0: The residuals are normally distributed.
Ha: The residuals are not normally distributed.
A low p-value (typically less than 0.05) indicates that you can reject the null hypothesis, meaning there's evidence that the residuals are not normally distributed.
The p-value 0.000 indicates that the model's residuals are not normally distributed.
The next step is to examine Residual Plots: histograms and other diagnostic plots of the residuals to visually assess their distribution.
Fit the model using the statsmodels OLS library
↪ 6. Potential Issues
Skew and Kurtosis Skewness measures the asymmetry of the distribution. A symmetrical distribution (like a normal distribution) has a skewness of 0.
Kurtosis measures the “tailedness” or “peakedness” of a distribution. A normal distribution has a kurtosis of 3.
The model has a positive skew and kurtosis > 3. The next step is to visualize the residuals with histograms and other diagnostic plots. These plots can help confirm the presence of skewness or kurtosis and provide more insight into the distribution.
Fit the model using the statsmodels OLS library
↪ 6. Potential Issues
Durbin-Watson The Durbin-Watson statistic shows the presence of autocorrelation in the residuals of an OLS regression model. The consequences of the existence of autocorrelation are
Autocorrelation refers to the lack of independence between values. The value of the Durbin-Watson statistic will lie between 0 and 4.
From the summary table, the Durbin-Watson statistic is 1.953. This means the data has no autocorrelation i.e. all observations are independent.
Fit the model using the statsmodels OLS library
↪ 6. Potential Issues
Jarque-Bera (JB) and Prob(JB) Similar to the Omnibus, the JB test checks if the residuals from the OLS model are normally distributed. The JB test calculates a statistic based on the skewness and kurtosis of the residuals.
The null and alternate hypotheses can be written as:
H0: The residuals are normally distributed.
Ha: The residuals are not normally distributed.
The p-value, Prob(JB), represents the probability of observing a JB statistic as extreme as the one calculated if the null hypothesis were true. A low p-value (usually less than 0.05) indicates strong evidence to reject the null hypothesis, suggesting that the residuals are not normally distributed.
The JB statistic of 66.459 indicates a large deviation from normality. The Prob(JB) of 3.70e-15 is less than 0.05, meaning reject the null hypothesis. Non-normal residuals might indicate issues like:
Fit the model using the statsmodels OLS library
↪ 6. Potential Issues
Cond. No. The “Cond. No.” (Condition Number) in OLS regression output measures a model's sensitivity to small changes in the data.
A low condition number (below 10) indicates a model that is less sensitive to small changes in the data. Conversely, a high condition number (generally above 10) suggests that even minor variations in the data can lead to significant changes in the estimated coefficients and other model outputs.
A high condition number often indicates multicollinearity, a situation where independent variables are highly correlated with each other. This can make it difficult for the model to accurately estimate the coefficients for individual predictors.
The condition number in this case is large, 2.09e+04. This might indicate that there is strong multicollinearity or other numerical problems.
Fit the model using the statsmodels OLS library
↪ 7. Residual Analysis
If a linear model makes sense, the
Fit the model using the statsmodels OLS library
↪ 7. Residual Analysis
Normal Distribution
The value of high kurtosis ( > 3 ) and Jarque-Bera (JB) number in the model indicates that the data has no normal distribution, i.e.and statistical analysis may perform poorly on the data.
A histogram of residuals and a normal probability plot of residuals can be used to evaluate whether the residuals are approximately normally distributed or not.
from scipy import stats mu, std = stats.norm.fit(lr.resid) fig, ax = plt.subplots() sns.histplot(x=lr.resid, ax=ax, stat="density", linewidth=0, kde=True) ax.set(title="Distribution of residuals", xlabel="residual") # # plot corresponding normal curve xmin, xmax = plt.xlim() # the maximum x values from the histogram above x = np.linspace(xmin, xmax, 100) # generate some x values p = stats.norm.pdf(x, mu, std) # calculate the y values for the normal curve sns.lineplot(x=x, y=p, color="orange", ax=ax) plt.show()
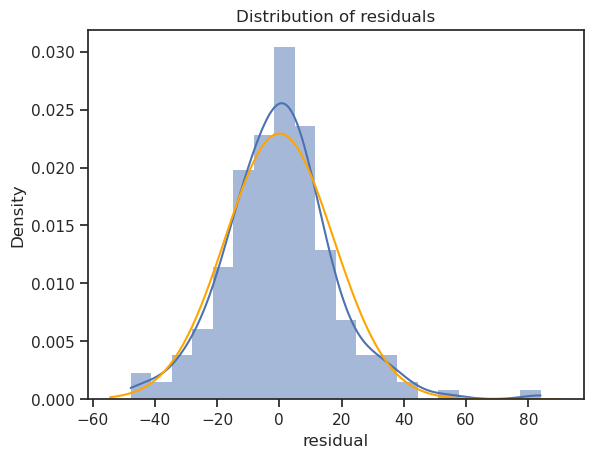
While the curve is slightly skewed, it has not deviated significantly from a normal distribution. Unless the residuals are substantially non-normal or exhibit a clear pattern, normality is not a major concern.
Fit the model using the statsmodels OLS library
↪ 7. Residual Analysis
Constant Variance
Homoscedasticity, also known as homogeneity of variances, describes a situation where the error term (or variance) in a regression model is constant across all values of the independent variables.
Heteroscedasticity (the violation of Homoscedasticity) is present when the size of the error term differs across values of an independent variable.
Breusch-Pagan test checks whether Heteroscedasticity exists in the regression model. The test follows the hypotheses below:
The null hypothesis is
H0 : Homoscedasticity is present (the residuals are distributed with equal variance)
Ha : Heteroscedasticity is present (the residuals are not distributed with equal variance)
from statsmodels.compat import lzip import statsmodels.stats.api as sms names = ['Lagrange multiplier statistic', 'p-value', 'f-value', 'f p-value'] test_result = sms.het_breuschpagan(lr.resid, lr.model.exog) print(lzip(names, test_result))
---Output--- # [('Lagrange multiplier statistic', 0.010023637585443446), # ('p-value', 0.9202505513848309), # ('f-value', 0.009923898577395387), # ('f p-value', 0.9207477833851023)]
The Lagrange multiplier statistic for the test is 0.01, with a corresponding p-value of 0.92. Since the p-value is greater than 0.05, we fail to reject the null hypothesis. This indicates that there is insufficient evidence to suggest heteroscedasticity in the regression model.
Heteroscedasticity can also be visually assessed by examining a scatterplot of residuals versus fitted values. In a homoscedastic model, the variance of the residuals should be constant across all values of the x-axis. This same scatterplot can also help to identify autocorrelation, which is discussed in the next section.
Fit the model using the statsmodels OLS library
↪ 7. Residual Analysis
Independence
Autocorrelation refers to the lack of independence between values. Durbin Watson statistic checks for the presence of autocorrelation in lag 1 of the residuals. The value of the statistic will lie between 0 to 4.
From the summary table, the Durbin-Watson statistic is 1.953. This means the data has no autocorrelation i.e. all observations are independent.
An existence of autocorrelation can be visualized with a scatter plot with residuals on one axis and the time component on the other axis. If the residuals are randomly distributed, there is no autocorrelation. If a specific pattern is observed, it indicates the presence of autocorrelation.
plt.scatter(y_train, lr.resid, c = "g", s = 60)
plt.hlines(y=0, xmin=1250, xmax=1750)
plt.title("Residual Plot")
plt.ylabel("Residual")
plt.show()
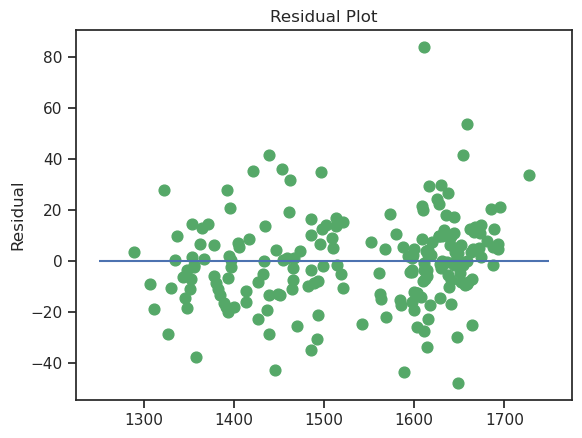
The points are randomly scattered, and it does not appear that there is a relationship.
A final note: Detecting residual patterns can improve the model.
Fit the model using the statsmodels OLS library
↪ 8. Predict and test the model
y_pred_ols = lr.predict(sm.add_constant(x_test)) y_pred = pd.DataFrame(y_pred_ols, columns=['Pred']) dframe = pd.concat([y_test.reset_index(drop=True).astype(float), y_pred.reset_index(drop=True).astype(float)], axis=1) dframe.columns = ['Actual','Predicted'] graph = dframe.head(10) print(graph)
---Output--- # - Actual Predicted # 0 1671.80 1665.338077 # 1 1617.65 1626.698965 # 2 1409.80 1404.276386 # 3 1600.65 1601.187244 # 4 1568.30 1599.304826 # 5 1644.10 1638.736535 # 6 1564.35 1570.622716 # 7 1389.55 1417.354240 # 8 1486.10 1442.667811 # 9 1590.90 1570.375029
Plot Graph
graph.plot(kind='bar')
plt.title('Actual vs Predicted')
plt.ylabel('Closing price')
plt.show()
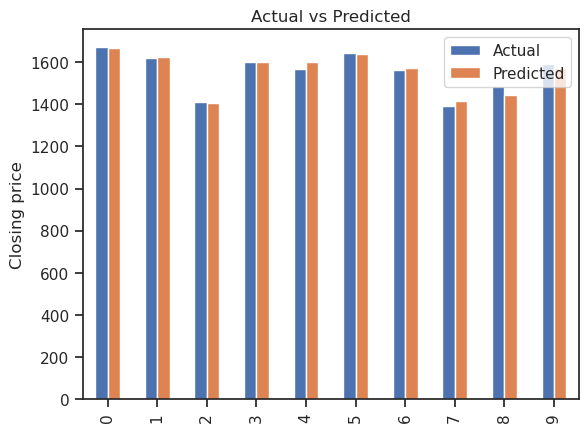
Fit the model using the statsmodels OLS library
↪ 8. Predict and test the model
Predicting Close Price
Predict_Close_Price= lr.predict(np.array([1,1508.80]))
print("Predicted Value: ", Predict_Close_Price)
---Output---
# Predicted Value: [1511.42561533]
